Template:Infobox mathematics function/sandbox2
Jump to navigation
Jump to search
| Gamma | |
|---|---|
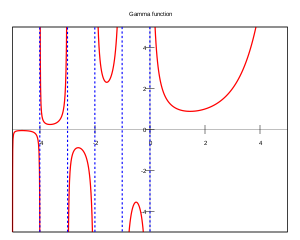 The gamma function along part of the real axis | |
| General Data | |
| General definition | <math> \Gamma(z) = \int_0^\infty x^{z-1} e^{-x}\,dx \ </math>,<math>\qquad \Re(z) > 0\ </math> |
| Deriver of General definition | Daniel Bernoulli |
| Motivation of creation | Interpolation for factorial function |
| Date of solution | 1720s |
| Extends | Factorial function |
| Fields of application | Probability, statistics, combinatorics |
| Main applications | probability-distribution functions |
| Domain and Range | |
| Domain | <math>\mathbb{C}</math> - ℤ0- |
| Codomain | <math>\mathbb{C}</math> - {0} |
| Basic features | |
| Parity | Not even and not odd |
| Period | No |
| analytic? | Yes |
| meromorphic? | Yes |
| holomorphic? | Yes except at ℤ0- |
| Specific values | |
| Maxima | No |
| Minima | No |
| Value at ℤ+ | <math>(n-1)!</math> |
| Value at ℤ0- | Not defined |
| Specific features | |
| Root | No |
| Critical point | <math>\supseteq</math> ℤ0- |
[[Inflection point|
| <math>\supseteq</math> ℤ0- |
| [[Fixed point (mathematics)|
| <math>\supseteq</math> 1 |
| Poles | <math>\supseteq</math> ℤ0- |
| Transform | |
| Corresponding transform | Mellin transform |
| Corresponding transform formula | <math> \Gamma(z) = \{ \mathcal M e^{-x} \} (z).</math> |
| The above documentation is transcluded from Template:Infobox mathematics function/sandbox2/doc. (edit | history) Editors can experiment in this template's sandbox (create | mirror) and testcases (create) pages. Please add categories to the /doc subpage. Subpages of this template. |