Template:Cantic table
Jump to navigation
Jump to search
| Symmetry *n32 [1+,2n,3] = [(n,3,3)] |
Spherical | Euclidean | Compact Hyperbolic | Paracompact | ||
|---|---|---|---|---|---|---|
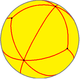
| *233 [1+,4,3] = [3,3] |
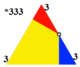
*333 [1+,6,3] = [(3,3,3)] |
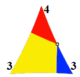
*433 [1+,8,3] = [(4,3,3)] |
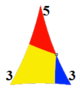
*533 [1+,10,3] = [(5,3,3)] |
*633... [1+,12,3] = [(6,3,3)] |
*∞33 [1+,∞,3] = [(∞,3,3)] | |
| Coxeter Schläfli |
h2{4,3} |
h2{6,3} |
h2{8,3} |
h2{10,3} |
h2{12,3} |
h2{∞,3} |
| Cantic figure |

|

|

|

|

|

|
| Vertex | 3.6.2.6 | 3.6.3.6 | 3.6.4.6 | 3.6.5.6 | 3.6.6.6 | 3.6.∞.6 |
 Domain |

|
|
|
|

|

|
| Wythoff | 2 3 | 3 | 3 3 | 3 | 4 3 | 3 | 5 3 | 3 | 6 3 | 3 | ∞ 3 | 3 |
| Dual figure |
|

|

|
|||
| Face | V3.6.2.6 | V3.6.3.6 | V3.6.4.6 | V3.6.5.6 | V3.6.6.6 | V3.6.∞.6 |
| Editors can experiment in this template's sandbox (create | mirror) and testcases (create) pages. Subpages of this template. |